La factorización es algo que muchas veces cuesta darse cuenta cuando emplearla, aunque también es complicado recordar algunos métodos que nos enseñan sin demostrar de donde viene (o normalmente la empleamos pero sin saber porque es así).
Por este motivo y muchos otros (que dan vuelta en mi cabeza) hoy les traigo la demostración de la diferencia de cuadrado a través de la geometría.
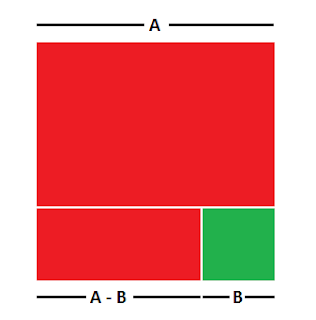
Lo que haremos es calcular el área de la región roja y como podemos apreciar podemos calcular de dos maneras, la primera calcular el área total y luego restar el área del cuadrado más pequeño (el de color verde)
Por lo tanto podemos escribir el área roja según la interpretación anterior:
La segunda manera, si nos ponemos a observar, si nos detenemos a observar, se puede sacar el área del rectángulo rojo pequeño y sumar con el área del rectángulo rojo mas grande
Por este motivo y muchos otros (que dan vuelta en mi cabeza) hoy les traigo la demostración de la diferencia de cuadrado a través de la geometría.
Lo que haremos es calcular el área de la región roja y como podemos apreciar podemos calcular de dos maneras, la primera calcular el área total y luego restar el área del cuadrado más pequeño (el de color verde)
Por lo tanto podemos escribir el área roja según la interpretación anterior:
Área roja = A2 – B2
La segunda manera, si nos ponemos a observar, si nos detenemos a observar, se puede sacar el área del rectángulo rojo pequeño y sumar con el área del rectángulo rojo mas grande
Área del rectángulo rojo mayor = A * (A - B)
Área del rectángulo rojo menor = B * (A - B)
ahora nos queda sumar las dos áreas y obtendremos el área roja:
Área roja = A * (A - B) + B * (A - B)
Sacamos factor común (A - B) y nos quedara que:
Área roja = (A - B) * (A + B)
y como dijimos en un principio (con el primer metodo) que el área roja = A2 – B2 , podremos decir que:
A2 – B2 = (A - B) * (A + B)
El producto de la suma de dos términos por su diferencia es igual a la diferencia de sus cuadrados.Nuevamente, espero que mis explicaciones se pueda entender, interpretar y de su agrado.
Comentarios
gracias
Publicar un comentario